日記

吉里吉里 v2.21 beta 4 からはジョイスティックが使える模様。ソースを見た限りでは、DirectInput使用してるみたい。内部実装だからプラグインよりも軽いだろうということで、こっちを採用。β版だけど気にしない。

タイマーイベントの発生タイミングがおかしい。インターバルを5msにしても16ms間隔でイベントが発生したり所々で31msになったり、20msにしても発生間隔が16ms, 31msごちゃ混ぜになったり。ディスプレイのリフレッシュレートの倍数と奇妙に一致しているのは気のせいか。

たかだかスプライト数256でCPUがヒーヒー言っていたのは、待ちイベントがエンキューされまくっていたせいかも。イベントキュー・キャパシティを1にすれば解決…かと思ったが、そううまくはいきません。

インターバルを16ミリ秒にして、イベント発生時刻と前回イベント発生時刻の差を採ってみた。

… 15 16 16 15 16 16 15 16 31 16 15 16 16 15 16 31 31 16 16 15 16 15 16 16 …

所々に31ミリ秒の空白ができており、その時におそらく一回分のイベントを採り逃しているものと思われる。タイマー周りのソースを読んだところ、enabledプロパティ変更時にタイマカウンタをリセットしているようなので、これを利用してみる。推奨できるやり方ではないが。

function onTimer() {
    timer.enabled = true;
    // ...
}

これをやると、結果的にタイマイベント1回につき1回分破棄されることになるようなので、16ミリ秒間隔でイベントを発生させたい場合はタイマオブジェクトのintervalを8msにしてやらないといけない。

… 15 16 15 16 16 15 16 16 15 16 15 16 16 15 16 16 15 16 15 16 16 15 16 16 …

稀に取りこぼして31msになることもあるが、頻度としては問題ないレベル。

timer.enabled = false は不要。というより、そもそもWindowsタイマの限界なのかも。

正弦を求めるのに、Math.sinを使った場合と正弦テーブルを使った場合とで実行速度を比較。最終的には角度も算出値も整数に正規化して使う予定なので、テーブルの方は予め正規化したものを使用。テーブルといってもただの配列(Array class)なので、当然こっちの方が圧倒的に速い。単純forループ（100万回）での測定で、Math.sinでの算出法より恒常的に3倍以上速かった。

明日は逆正接テーブル。逆正接は正規化が面倒なんだよなー。

三角形が大好きな良い子のみんなは三角関数と聞くと円を連想するが、ここでは円の出番はない。

直交座標軸に平行な、一辺の長さがNの正方形の左下の点をO、右下、右上、左上の点をそれぞれA、B、Cとする。点Pが線分AB上にあるとき、APの長さをa、角POAの大きさをθとすると、

θ = arctan(a/N) .

点Pが、点Cを除く線分BC上にあるとき、CPの長さをcとすると、

θ = arctan(N/c) .

点Pが点Aから点Bを経由して点Cまで移動するとき、点P(px, py)の位置が離散的、つまりpx, pyが整数値しか取らないとすると、点Pの取りうる位置は (N, 0), (N, 1), ..., (N, N-1), (N, N), (N-1, N), (N-2, N), ..., (1, N), (0, N) の2N + 1箇所。それぞれの点をP[0], P[1], ..., P[2N]とするとき、各点P[n]における角θ[n]は下記の通り。

px > py (n < N) のとき

θ[n] = arctan(n/N)

0 < px <= py (n >= N) のとき

θ[n] = arctan(N/n)

px = 0 (n = N) のとき

θ[n] = π/2

θ[n]を要素数2N+1の配列と見なして、第一象限の逆正接テーブル完成。

何で「象限」を変換できないんだMS-IME。

第一象限上のある点をE(x, y)、角EOAをωとすると、

ω = θ[m]

が成り立つ。mは配列θにアクセスするためのインデックスであり、以下に示すxとyの関数Mによって定まる。 ^*1

x > y のとき

int( Ny/x )

0 < x <= y のとき

int( N(2-x/y) )

x = 0 のとき

2N

以上をまとめると、

ω = θ[M(x, y)]

となる。第二、第三、第四象限についても基本的に同じなので省略。

これを関数化して、

function arctangent(x, y) {
  // ... 面倒なので省略
  return omega;
}

といった感じ。

しかし、実はインデックスを求めるM(x, y)には、象限による分岐、xとyの大小関係による分岐、ほとんどのケースで必要となる乗算＆除算など、意外と重い処理になってしまうという大きな落とし穴がある。これをどう回避するか、元を辿ればインデックスと角度の関係をどうするかによって arctangent(x, y) の実行速度は変わってくる。下手をすると、インデックス値の算出に膨大な時間を消費してしまい、Math.atan() 一発の方が速いという目も当てられない状態にもなりかねない。

続きは明日。

ディスプレイのリフレッシュレートの倍数と奇妙に一致しているのは気のせいでした。が、インターバルを5msにしても22msにしても、15msか16msの倍数単位でイベントが起こる。Timerの精度がnormalだからなのだろうが、精度を上げるとCPU負荷も上がるしなあ。

-waitvsync や -dbstyle を使用するとCPUの負荷が急上昇。反って動作が重くなった。X680x0だったらI/Oポートを直接叩けば垂直同期待ちが簡単にできるんだけどなー。とか言ってもしょうがないんだけど。

第一象限上の点については算出可能なので、次は座標上の任意の点F(x, y)について考えてみる。逆正接テーブルは、全象限に対応したものが作成されているとして話を進める。第一象限のケースでは、正方形OABC上の点P（つまりインデックス）はA→B→Cと、原点Oを中心に左回りに進むものとしているが、他の象限でも同様に左回りとする。

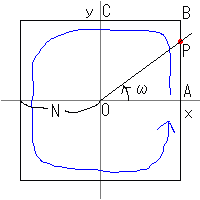
インデックスの算出方法はいくつかあるだろうが、ここではx, yの絶対値を使ってインデックスmを求める。

まずはx=0またはy=0のケースを特例として扱い、除外する。

x = 0, y >= 0 のとき

m = 2N

x = 0, y < 0 のとき

m = 6N

x >= 0, y = 0 のとき

m = 0

x < 0, y = 0 のとき

m = 4N

次にx, yの絶対値を元に仮のインデックスm'を求める。この計算式は、第一象限でのケースと基本的に同じである。 ^*1

abs(x) > abs(y) のとき

m' = abs(int( Ny/x ))

abs(x) <= abs(y) のとき

m' = abs(int( N(2-x/y) ))

最後にm'を、F(x, y)の位置（象限）によって補正し、インデックスmを求める。

x > 0, y > 0 （第一象限）のとき

m = m'

x < 0, y > 0 （第二象限）のとき

m = 4N - m'

x < 0, y < 0 （第三象限）のとき

m = 4N + m'

x > 0, y < 0 （第四象限）のとき

m = 8N - m'

実際のコーディングにおいては整数演算のみになるだろうから、乗算と除算の入り混じっている箇所では演算順序に注意して精度を保つようにする。以上。

…さすがにこれだけの分岐があると、辛いかも。コーディング量がそのままパース量に跳ね返ってくるわけだし。10回や20回の実行ならともかく、秒間数千回も実行されるような場合は少なからずCPUパワーを殺ぐ事になるわけで。

ちなみに、このテーブルの長所は、参照時に実数演算が不要なことと、（整数の割には）精度がかなり高いこと。短所は、インデックスの算出が面倒なこと。

逆正接テーブルのインデックス算出をTJS2でやるのもなんだし、DLL形式のプラグイン制作の練習も兼ねて、吉里吉里プラグインを作ってみた。テンプレートを作っておき、新規にプラグインを作るときはテンプレートから起こすのが楽だろう。

• Borland C++ 5.5.1 for Win32 をセットアップ。
• （吉里吉里のソース） base\win32\plugin_kit\, base\win32\plugin_kit\basetest\ にある tp_stub.cpp, tp_stub.h, Main.cpp, basetest.mak を、適当なディレクトリ（仮にtemplate）にコピー。
• basetest.mak のファイル名を makefile に変更（…しなくてもいいけど）。
• makefile を適当に書き変える。PASCAL関係とかIDE関係は基本的に不要。VCL50.LIBは微妙。
• Main.cpp を適当にシェイプアップ。
• make

ちゃんとDLLが作成されたら、テンプレートの出来上がり。テンプレートとしては、吉里吉里ソースからコピー＆改変した4ファイル以外は不要なので、それらを削除。新規にプラグインを作成するときは、このディレクトリを丸ごと新規ディレクトリにコピーして、それを叩き台にすればよい。

以前JAVAで作ったブレゼンハム関連のソースを、TJS2に移植。たいした量じゃないのですぐに終わる。何でこんなものが要るのかといえば、線分を描く関数を作るためで、実は吉里吉里(v2.21beta8)には線分を描く機能がなかったりする。また、円を描くことも点を打つことも、標準ではできない。あるのは矩形塗りつぶしのみ ^*2 。無いものは作るということで、TJS2で実装。だが遅い。

ブレゼンハムのロジックそのものはC++で実装して処理速度を稼いでもいいが、いかんせん描画そのものが遅い（矩形だし）ので、全体的な速度向上にはならないかも。まあ、ブレゼンハムのアレはほかにも使い道があるから、プラグインとして作っておいても無駄にはなるまい。

…プラグイン関数から配列を返すにはどうすればいいのかな。

調子に乗って円を描く関数も作る。これはミッチェナーのアルゴリズム。某ソースからのパクり。

プラグインを改良。逆正接テーブルをDLL内部に持つことで、TJS2側からはarctan(x, y)みたいに呼べるようになった。単純にコールするだけだと、TJS2関数のMath.atan()よりも二割ほどしか速くないが、実戦においては、Math.atan()はコールしたあとに象限判定や整数補正などの処理を追加しなければならないため、実戦での速度パフォーマンスは数倍〜十数倍の差が出るだろう。実際、Math.atan()に単純な整数補正を加えただけでも4倍ほどの差が出た。まあ、用途が特化、限定されているから、汎用のものより速くなるのは当然なんだけど。

ついでに、正弦と余弦、距離算出関数も追加。距離算出には、平方根を使わない方法にした。原点と点(x, y)との距離は、三平方の定理からSQRT(x^2 + y^2)で求められるが、平方根計算は嫌なので、x / cos(arctan(y/x))でやる。cosもarctanもテーブル化してあるからさほど重くはないだろう。

吉里吉里プラグインとして関数を作成するときには、関数一つにつきクラスを一つ作ることになるので、コードを書くのがちょっと面倒。また、プラグインリンク時、アンリンク時の手続きも少々面倒なのだが、決して難しいわけではない。吉里吉里にはコメントのたくさん入ったわかりやすいテンプレートがあるから、それを真似、というかほとんどコピーすれば、割と簡単にプラグインを作れる。このあたり、開発者にやさしいと思うのだが、どうだろう。

プラグイン関数から配列を返すのではなくて、プラグイン関数にTJS2 Arrayオブジェクトへの参照を引数で渡し、プラグイン関数はその参照に対して操作を行う、という形式ならいけるかも。

Plugins.link("foo.dll");とするとネイティブクラスFooを使えるようになってTJS2からvar foo = new Foo();みたいに呼べるといいなと思ってTJS2ネイティブクラスを実装しようとしたが、C++名前空間の壁とかいろんなものに阻まれて撃沈。少なくとも、既存のプラグイン作成テンプレートそのままでは使えないようだ。

憂さ晴らしに矩形接触判定関数を作る。接触しない条件を考えてみれば話は簡単。

マニュアルを読んでいたところ、iTJSDispatch2を実装すればできそうな気がしてきた。明日、じっくりやってみよう。

吉里吉里2.21beta8のソースを読んでいたら、drawLine() なる関数を発見。ずばり、レイヤーに直線を描画するプラグイン関数のようだが、完全に実装されてないように見える。Blurの使いまわしのような…

こいつを雛型にするくらいのことはできそう。C++内でのレイヤーオブジェクトの扱い方は参考になるかも。

DLLプラグインでクラスを。

tTJSDispatchを継承してゴニョゴニョすれば何とかなりそうなのだが、「ゴニョゴニョ」の具体的な内容が見えてこない。天下のGoogle様で検索したり、いいサンプルはないかと吉里吉里ソースをひっくり返して探してみたりしたが、見つからなかった。CreateNew()を実装することが、クラスオブジェクトとして振舞うための初めの一歩だと思うのだが…わからないことがたくさん。メソッドをFuncCall()で受け取ったときの振る舞い方――FuncCallByNum()のラッパーとして振舞えばよいのだろうか――、これもよくわからないし。むー。